The following discussion of operations is not intented to be complete, and several of the more arcane or complex functions are not detailed here. For these, see either the documentation or have a look in the include files (especially tensor.h). All functions, like the whole rest of the code, reside in the tensor namespace. Consequently, you either have to prepend all functions here with "tensor::", or import them or the whole tensor namespace with a using-directive.

Tensor shapes and ranks

In some applications, the actual shape of a tensor should be modified without modifying the content. Similar to their Matlab counterparts, the reshape() function gives a tensor an arbitrary shape, and squeeze() removes dimensions of size 1. To modify the dimensions of a tensor, the permute() function swaps two indices of a tensor, also modifying the content.

CTensor a = CTensor::random(5, 4);
CTensor b = reshape(a, 1, 2, 2, 5); // b is a 1x2x2x5 tensor with the same data as a
CTensor c = squeeze(b);             // c is now a 2x2x5 tensor
CTensor d = permute(a, 0, -1);      // swaps first and last index, d(i,j) == a(j,i)

Unary Tensor operations

The library contains a limited number of unary elementwise operators for tensors. These include negation (- A) and special functions (cos(), exp(), sqrt() etc). For complex tensors, common operations are also supported (abs(), conj(), real(), imag()).

Binary Tensor operations

The library supports various operations between tensors. Elementwise addition, subtraction, multiplication and division are implemented. Furthermore, it is possible to compare tensors via all standard operators (==, < etc.). The result of such comparisons is a vector of booleans that holds the result for each element. If two tensors should be compared for exact equality, you can also use the functions all_equal() and some_unequal().

Contractions, scaling and tracing

Tensor contractions constitute a generalization of matrix multiplication for tensor with more than two indices and come in two flavors.

The first flavor is "exterior" contraction, in which the indices of the tensor are simply joined together. This is done with the function fold(), which takes four arguments, as in fold(A, nA, B, nB). The two arguments A and B are two tensors, while nA and nB represent the indices that are contracted.

For instance, assuming that A has two and B three indices, the code C=fold(A,0,B,1) contracts the second and first index of tensors A and B, respectively, as given by the formula

$C_{a_1 b_0 b_2} = \sum_j A_{j a_1} B_{b_0 j b_2}$

Note that the indices of B are simply added to those of A, in that precise order.

The other flavor is "internal" contraction, in which indices are replaced. Going back to the previous example, C=foldin(A,0,B,1) contracts tensors A and B according to the formula

$C_{b_0 a_1 b_2} = \sum_j A_{j a_1} B_{b_0 j b_2}$

Now the uncontracted indices of A appear in the place of the contracted index of B. This routine is very useful for applying transformations on certain indices of a tensor. Typically, A is a matrix describing an operator that only modifies the index / degree of freedom j.

Various derivates of these functions exist. The routine foldc() uses the complex conjugate of A for the contraction. The routines fold_into() and foldin_into() allow you to specify the target tensor as the first element. This is useful to avoid expensive memory allocation if you already have a fitting tensor for C lying around.

Another operation that can be done with tensors is scaling. For a tensor A with, say, three indices and a one-dimensional tensor (vector) V, the expression C=scale(A,2,V) scales A according to the formula

$C_{a_0 a_1 a_2} = A_{a_0 a_1 a_2} V_{a_2}$

A variant scale_inplace exists that stores the result of the scaling directly in A.

Finally, you can trace out indices. For a tensor A with three indices, the function C=trace(A,0,2) calculates C as

$C_{k} = \sum_i A_{i k i}$

Tensor reductions

Various functions allow the reduction of one or two tensors to a single value. The functions sum() and mean() return the expected sum or mean value of all tensor entries.

The scalar product scprod(A,B) of two tensors A, B (interpreted as one-dimensional vectors of numbers) is given by

$\sum_i A_i B_i^\ast$

Two norms are provided: A maximum norm norm0(A) returns the entry of A with the largest absolute value. The usual L2-norm, norm2(A) is equivalent to the expression sqrt(scprod(A,A)).

Matrix operations

For matrices, i.e., tensors of rank two, there are a few specialized functions. The multiplication of two matrices A, B is a special case of tensor contractions, and is implemented by the function mmult(A,B).

You can take a vector V, and build from this a matrix by interpreting the values of V as the diagonal of a matrix. The code A=diag(V,-1,5,6) returns a 5x6 matrix that is zero except for the first side diagonal, which contains the elements of V, i.e., 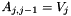$A_{j, j-1} = V_{j}$ ).

For the special case of matrices, there are also the functions transpose() and adjoint(). Furthermore, a convenience trace() function is supplied that takes only the matrix as parameter and returns the matrix trace.

Further operations

There are also a couple of further functions for complex manipulations.

The namespace linalg (header linalg.h) contains various linear algebra decomposition routines for matrices. There are also routines for Fast Fourier Transformations of tensors along arbitrary indices (header fftw.h). These functionalities may only be available with special configuration options, though.