Data Structures
class	linalg::CArpack
	Finder of a few eigenvalues of eigenvectors via Arnoldi method. More...

class	linalg::RArpack
	Finder of a few eigenvalues of eigenvectors via Arnoldi method. More...

Functions
const CTensor	linalg::eig (const RTensor &A, CTensor R=0, CTensor L=0)
	Eigenvalue decomposition of a real matrix. More...

const CTensor	linalg::eig (const CTensor &A, CTensor R=0, CTensor L=0)
	Eigenvalue decomposition of a complex matrix. More...

double	linalg::eig_power_left (const RTensor &O, RTensor *vector, size_t iter, double tol)
	Left eigenvalue and eigenvector with the largest absolute value, computed using the power method.

tensor::cdouble	linalg::eig_power_left (const CTensor &O, CTensor *vector, size_t iter, double tol)
	Left eigenvalue and eigenvector with the largest absolute value, computed using the power method.

double	linalg::eig_power_right (const RTensor &O, RTensor *vector, size_t iter, double tol)
	Right eigenvalue and eigenvector with the largest absolute value, computed using the power method.

tensor::cdouble	linalg::eig_power_right (const CTensor &O, CTensor *vector, size_t iter, double tol)
	Right eigenvalue and eigenvector with the largest absolute value, computed using the power method.

RTensor	linalg::eig_sym (const RTensor &A, RTensor *V)
	Eigenvalue decomposition of a real matrix. More...

RTensor	linalg::eig_sym (const CTensor &A, CTensor *V)
	Eigenvalue decomposition of a complex matrix. More...

const RTensor	linalg::expm (const RTensor &Aunorm, unsigned int order)
	Compute the exponential of a real matrix. More...

const CTensor	linalg::expm (const CTensor &Aunorm, unsigned int order)
	Compute the exponential of a real matrix. More...

const RTensor	linalg::solve (const RTensor &A, const RTensor &B)
	Solve a real linear system of equations by Gauss-Seidel method. More...

const CTensor	linalg::solve (const CTensor &A, const CTensor &B)
	Solve a complex linear system of equations by Gauss-Seidel method.

const RTensor	linalg::solve_with_svd (const RTensor &A, const RTensor &B, double tol)
	Solution of a linear system of equations using Penrose's pseudoinvese. More...

const CTensor	linalg::solve_with_svd (const CTensor &A, const CTensor &B, double tol)
	Solution of a linear system of equations using Penrose's pseudoinvese. More...

RTensor	linalg::svd (RTensor A, RTensor U, RTensor VT, bool economic)
	Singular value decomposition of a real matrix. More...

RTensor	linalg::svd (CTensor A, CTensor U, CTensor VT, bool economic)
	Singular value decomposition of a complex matrix. More...

Detailed Description

Function Documentation

const CTensor linalg::eig	(	const RTensor &	A,
		CTensor *	R = `0`,
		CTensor *	L = `0`
	)

Eigenvalue decomposition of a real matrix.

Given a square matrix A, we find a diagonal matrix D and a set of vectors R or L such that A R = R D or L A = D L

The eigenvalue decomposition is computed using the DGEEV routine from the LAPACK library. By default, only the diagonal elements of S are computed. However, also the U and V matrices can be computed if pointers to the associated variables are supplied.

Definition at line 45 of file eig_d.cc.

const CTensor linalg::eig	(	const CTensor &	A,
		CTensor *	R = `0`,
		CTensor *	L = `0`
	)

Eigenvalue decomposition of a complex matrix.

Given a square matrix A, we find a diagonal matrix D and a set of vectors R or L such that A R = R D or L A = D L

The eigenvalue decomposition is computed using the ZGEEV routine from the LAPACK library. By default, only the diagonal elements of S are computed. However, also the U and V matrices can be computed if pointers to the associated variables are supplied.

Definition at line 47 of file eig_z.cc.

RTensor linalg::eig_sym	(	const RTensor &	A,
		RTensor *	V
	)

Eigenvalue decomposition of a real matrix.

Given a square matrix A, we find a diagonal matrix D and a set of vectors R or L such that A V = V D and transpose(V) A = D transpose(V)

The matrix A must be symmetric (transpose(A)==A).

By default, only the diagonal elements of D are computed. However, also the matrix V can be computed if a pointer to the associated variable is supplied.

Definition at line 44 of file eig_sym_d.cc.

RTensor linalg::eig_sym	(	const CTensor &	A,
		CTensor *	V
	)

Eigenvalue decomposition of a complex matrix.

Given a square matrix A, we find a diagonal matrix D and a set of vectors R or L such that A V = V D and adjoint(V) A = D adjoint(V)

The matrix A must be Hermitian (adjoint(A)==A).

By default, only the diagonal elements of D are computed. However, also the matrix V can be computed if a pointer to the associated variable is supplied.

Definition at line 44 of file eig_sym_z.cc.

const RTensor linalg::expm	(	const RTensor &	Aunorm,
		unsigned int	order
	)

Compute the exponential of a real matrix.

This function computes the exponential of a matrix using a Pade approximation of any given order.

This is potentially more accurate than using the eigenvalues of the matrix or a Taylor expansion of the exponential, and much faster, since it only involves products of matrices and solving one system of equations.

The current algorithm has been adapted from Scientific Python, the version written by Travis Oliphant (2002). It is slightly more accurate than the same Matlab version when computed with the default order of 7.

Definition at line 42 of file expm_d.cc.

const CTensor linalg::expm	(	const CTensor &	Aunorm,
		unsigned int	order
	)

Compute the exponential of a real matrix.

This function computes the exponential of a matrix using a Pade approximation of any given order.

This is potentially more accurate than using the eigenvalues of the matrix or a Taylor expansion of the exponential, and much faster, since it only involves products of matrices and solving one system of equations.

The current algorithm has been adapted from Scientific Python, the version written by Travis Oliphant (2002). It is slightly more accurate than the same Matlab version when computed with the default order of 7.

Definition at line 40 of file expm_z.cc.

const RTensor linalg::solve	(	const RTensor &	A,
		const RTensor &	B
	)

Solve a real linear system of equations by Gauss-Seidel method.

Given a matrix A, and a right hand matrix B, we find the matrix X that satisfies A X = B using the LU factorization.

The solution is computed using the DGESV/ZGESV routines from LAPACK.

Definition at line 39 of file solve_d.cc.

const RTensor linalg::solve_with_svd	(	const RTensor &	A,
		const RTensor &	B,
		double	tol
	)

Solution of a linear system of equations using Penrose's pseudoinvese.

This function solves the system of equations A * X = B using the SVD of the matrix A = U * S * VT, through the formula X = V * (S^-1) * UT * B. When computing (S^-1), singular values below the tolerance are discarded.

Definition at line 37 of file solve_with_svd_d.cc.

const CTensor linalg::solve_with_svd	(	const CTensor &	A,
		const CTensor &	B,
		double	tol
	)

Solution of a linear system of equations using Penrose's pseudoinvese.

This function solves the system of equations A * X = B using the SVD of the matrix A = U * S * VT, through the formula X = V * (S^-1) * UT * B. When computing (S^-1), singular values below the tolerance are discarded.

Definition at line 37 of file solve_with_svd_z.cc.

RTensor linalg::svd	(	RTensor	A,
		RTensor *	U,
		RTensor *	VT,
		bool	economic
	)

Singular value decomposition of a real matrix.

The singular value decomposition of a matrix A, consists in finding two unitary matrices U and V, and diagonal one S with nonnegative elements, such that 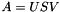$A = U S V$ . The svd() routine computes the diagonal elements of the matrix S and puts them in a 1D tensor, which is the output of the routine. Optionally, the matrices U and V are also computed, and stored in the variables pointed to by U and VT.

Unless otherwise specified, if the matrix A has MxN elements, then U is MxM, V is NxN and the vector S will have min(M,N) elements. However if flag economic is different from zero, then we get smaller matrices, U being MxR, V being RxN and S will have R=min(M,N) elements.

Definition at line 50 of file svd_d.cc.

RTensor linalg::svd	(	CTensor	A,
		CTensor *	U,
		CTensor *	VT,
		bool	economic
	)

Singular value decomposition of a complex matrix.

The singular value decomposition of a matrix A, consists in finding two unitary matrices U and V, and diagonal one S with nonnegative elements, such that 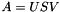$A = U S V$ . The svd() routine computes the diagonal elements of the matrix S and puts them in a 1D tensor, which is the output of the routine. Optionally, the matrices U and V are also computed, and stored in the variables pointed to by U and VT.

Unless otherwise specified, if the matrix A has MxN elements, then U is MxM, V is NxN and the vector S will have min(M,N) elements. However if flag economic is different from zero, then we get smaller matrices, U being MxR, V being RxN and S will have R=min(M,N) elements.

Definition at line 45 of file svd_z.cc.

Data Structures

Functions

Detailed Description

Function Documentation